
ネコでも分かる!伝家の宝刀セグメントツリー
はじめに
みなさんこんにちは、ALH開発事業部のREIYAです。
今回はネコでも分かるように簡単にセグメントツリーの解説と実装をしていこうと思います。
なお筆者はネコを飼っていませんので、ほんとうにネコでも分かるかどうかは未検証です。
おことわり
非再帰版で、抽象化まで書きました。
またひとえにセグメントツリーといってもいろいろありますが、世間でよく言われているセグメントツリーを取り上げています。
なるべく簡単に伝わるように、ビット演算や行数を圧縮するような書き方をしないようにしています。
一番下にガッツリ圧縮した版や、構造体にした版も貼っておきますので、まずはスラスラ実装できるように理解することを目的としています。
また先人たちが多く似たような記事を書いていますが、なるべく簡単に理解できるように心がけていますので是非読んでやってください。
セグメントツリーとは?
1点更新と区間取得ができるデータ構造です。
例えば以下のような配列で
更新
↓
1, 2, 3, 4, 5, 6, 7, 8
<-------->
この区間の和(1-indexedで)2番目から5番目の和は?最小値は?などを求めつつ、5番目の値を更新することもできます。
これにより区間に対する操作、俗に言う区間クエリを高速に処理することができます。
ちなみにセグメント木、セグ木などとも呼ばれます。
配列で十分なのでは?
計算量を知っていますか?
区間の最小値、区間の和などを求める場合
区間の要素数がN個である時、forループでN周すれば求まります。
list = [1, 2, 3, 4, 5, 6, 7, 8]
sum = 0
for v in range(2, 6): # N周
sum += list[v]
print(sum) # 3 + 4 + 5 + 6 = 18よって計算量は$${O(N)}$$です。
一方セグ木では$${O(logN)}$$で求まります。どこからlogが出てくるのかは仕組みを理解すると納得できますので慌てずに。
実際、$${N = 10^8}$$ほどだった場合、$${log_210^8=26.575424759099...}$$ですので、30回もループせずに済みます。愚直にやると1億回。これってすごくないですか?いったいどんな魔法が使われているのでしょうか。
実はただの配列をうまいこと使っているだけなんです。なので言葉の綾ですが、実際配列で十分ではあります。
さっさと実装を!
以下がセグメントツリーです。PythonとC++で用意しました。
一点を更新し、区間の最小値を求めています。
まずは眺めてみましょう。パッと見で、そんなに難しいことはしていなさそうに見えませんか?
dat = [1, 3, 2, 9, -10, 2, 1, 0]
size = len(dat)
segment_tree = [1e9] * size * 2
# 葉に値を詰めます
for i in range(size):
segment_tree[i + size] = dat[i]
# 葉から親に
for i in reversed(range(size)):
# 親からみた子2人
child_1 = segment_tree[i * 2]
child_2 = segment_tree[i * 2 + 1]
# 小さい方を親とする
segment_tree[i] = min(child_1, child_2)
# 一点更新
idx = 3 # 9から3へ変更
new_value = 3
# まずはその葉を更新
leaf = idx + size;
segment_tree[leaf] = new_value
while leaf != 0:
leaf //= 2
# 親からみた子2人
child_1 = segment_tree[leaf * 2]
child_2 = segment_tree[leaf * 2 + 1]
# 小さい方を親とする
segment_tree[leaf] = min(child_1, child_2)
# 区間取得
product = 1e9;
left = 2 # idx: 2から
right = 5 + 1 # idx: 5までを取得
left += size
right += size
while left < right:
if left % 2 != 0:
product = min(product, segment_tree[left])
left += 1
if right % 2 != 0:
right -= 1
product = min(product, segment_tree[right])
left //= 2
right //= 2
print(product)#include <iostream>
#include <vector>
int main() {
std::vector<int> A = {1, 3, 2, 9, -10, 2, 1, 0};
int length = A.size();
std::vector<int> segment_tree(length * 2, 1e9);
// 葉に値を詰めます
for (int i = 0; i < length; ++i) {
segment_tree[i + length] = A[i];
}
// 葉から親に
for (int i = length - 1; i >= 0; --i) {
// 親からみた子2人
int child_1 = segment_tree[i * 2];
int child_2 = segment_tree[i * 2 + 1];
// 小さい方を親とする
segment_tree[i] = std::min(child_1, child_2);
}
// 1点更新
int idx = 3; // 9から3へ変更
int new_value = 3;
// まずはその葉を更新
int leaf = idx + length;
segment_tree[leaf] = new_value;
while (leaf != 0) {
leaf /= 2;
// 親からみた子2人
int child_1 = segment_tree[leaf * 2];
int child_2 = segment_tree[leaf * 2 + 1];
// 小さい方を親とする
segment_tree[leaf] = std::min(child_1, child_2);
}
// 区間取得
int product = 1e9;
int left = 2; // idx: 2から
int right = 5 + 1; // idx: 5までを取得
left += length;
right += length;
while (left < right) {
if (left % 2 != 0) {
product = std::min(product, segment_tree[left]);
left++;
}
if (right % 2 != 0) {
--right;
product = std::min(product, segment_tree[right]);
}
left /= 2;
right /= 2;
}
std::cout << product << std::endl;
}仕組みの解説
ゆっくりみていきましょう。以下の配列での、区間の最小値を求めることを考えます。
dat = [1, 3, 2, 9, -10, 2, 1, 0]まずはセグメント木の思想です。こうしたいんです。

明らかにいちばん小さい-10を赤くしておきました。
...は?って感じですよね。手元のスプレッドシートなどで、これを書いてみてください。どういう順番で埋めましたか?
まず黄色を埋めたあと、ひとつ上の段を埋めますよね?
した二つのうち小さい方と見るんです。
この図はわかりましたね?
だからどういう意味があるんだと思うでしょう。焦らないでください。ゆっくりみていきます。
さて、もうちょっと図をわかりやすくしましょう。さっきの図はこう書いてもよいですね?
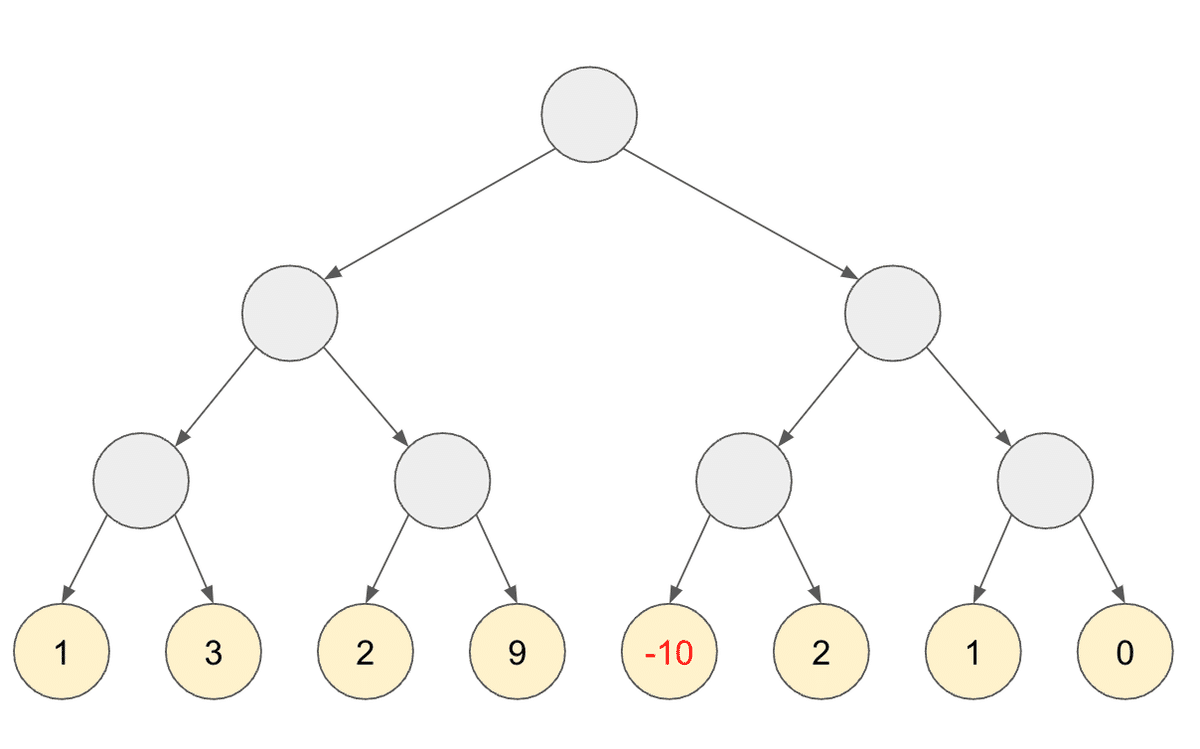
なんか木っぽくないですか!?逆さまですけども!!
これをグラフ理論では木と呼びます!
一つの丸から、2個ずつ綺麗に生えてますね?
これを木の中でも、完全二分木と言います。(厳密には「すべての葉が同じ深さを持ち、すべての内部節点の次数が 2 であるような二分木」)
まぁ難しいことはいいんです。これをみて綺麗だなと思えたら勝ちです。
この時、以下のように、親、子と呼びます。

また、ここを根、葉と呼びます。

前置きはこれくらいにして、仕組みを覗いていきましょう。
大事なのは2つ。
前もって持っておく
必要な部分だけを取得する
ではいきます。
1. 前もって持っておく
なんで計算量が少なく済むかというと、あらかじめ答えを持って置いてるからです。
先ほどの木を埋めることを考えます。まずは配列のインデックスと紐づけて考えます。

インデックスをつけて、値もうめときました。ちなみに都合がいいので1-indexdにします。index 0番は使いません。贅沢。
さて、重要な考察。2個注目します。
インデックス青いとこあるよ?
値どうやってうめた?
まずはインデックス青から。
勘のいいガキのみなさん(ハガレン)はもうお気づきかと思います。
そうです。2のべき乗です。左側が綺麗に2のべき乗になっているんです。これがとてもありがたい性質を持っています。
では値どうやって埋めた?まずはここを見ましょう。

インデックス4の親には、インデックス8と9の子の、小さい方を渡しました。
他も見てみます。
インデックス5の親は、子が10と11です。
インデックス2は、子が4と5です。
6の子は12、13
7の子は14、15
...
何かに気が付きましたか?
そうです。親の子2人は、2倍と2倍+1なんです。
また子から親に行くには2で割る(切り捨て) です。
あとインデックスは、子の左は偶数で、右が奇数です。
これがセグ木の本質部分です。
当たり前なような気がしますか?これが2ベキのありがたみです。
もう一つ重要な性質。元の配列の長さは8でした。
この木の要素は15個です。
葉以外で、8 - 1個使っています。無駄にしているインデックス0を含めれば
木の配列サイズは元のちょうど2倍です。
ふむふむ。
2倍サイズの配列でもち、葉に元配列の値をいれて、親は子の2倍、2倍+1だから、作りたい配列って、元配列のインデックスにサイズ分ゲタを履かせたようなイメージですね。

こちらは尊厳を奪われ、ただの直線に並べられたセグメント木さんです。ただの配列なんです。これを木のように見立てていただけというわけです。
これをプログラムで書いてみましょう(唐突)簡潔のためにPythonで書きます。
まずは2倍サイズの配列を作ります。
dat = [1, 3, 2, 9, -10, 2, 1, 0]
# 2倍サイズの配列
size = len(dat)
segment_tree = [1e9] * size * 21e9 (10の9乗、32bit整数で大きめの数です)を入れているのは
1e9と5で小さい方って5でしょ?
小さい方、を考えるにあたって絶対無視できる数が欲しくて、適当に大きい値を入れています。(詳しくは深い話があるので後ほど。)
ちなみにここがC++だと
std::vector<int> segment_tree(length * 2, 1e9);です。冒頭のソースと照らし合わせたい方むけ。
で、葉に元配列の値いれる。葉は下駄を履かせていますので、0~sizeのループ中なら、i + sizeで葉になりますね。
# 葉に値を詰めます
for i in range(size):
segment_tree[i + size] = dat[i]よしよし。ここまでまとめると
dat = [1, 3, 2, 9, -10, 2, 1, 0]
size = len(dat)
segment_tree = [1e9] * size * 2
# 葉に値を詰めます
for i in range(size):
segment_tree[i + size] = dat[i]
print(segment_tree)[1000000000.0, 1000000000.0, 1000000000.0, 1000000000.0, 1000000000.0, 1000000000.0, 1000000000.0, 1000000000.0, 1, 3, 2, 9, -10, 2, 1, 0]こうなりました。
よーし、じゃあ次は2個のうち小さい方を埋めていく作業ですね。
いま、配列のうしろ半分を葉で埋めたので
今度は、前半分を埋めればいいですね?
ということはループ範囲は1からsizeあたりです。が、
こういうふうに右下から順番で埋めたいです。葉から吸い上げるように値を埋めていきましょう。

よって、たどるインデックスは、7, 6, 5, 4, 3, 2, 1です。
これはつまり、size - 1から1までの逆向きループですね。
(0もやっちゃってますが、どうせ使わないので0まで行っていいよ)
# 葉から親に
for i in reversed(range(size)):
# 親からみた子2人
child_1 = segment_tree[i * 2] # 2倍
child_2 = segment_tree[i * 2 + 1] # 2倍+1
# 小さい方を親とする
segment_tree[i] = min(child_1, child_2)これによりsegment_treeの中身が
[-10, -10, 1, -10, 1, 2, -10, 0, 1, 3, 2, 9, -10, 2, 1, 0]となっていればOKです。
これによって、晴れてセグメント木を構築できました。すばらしいです。お疲れ様です。
休憩する前に、葉を1枚更新しちゃいましょう。
簡単です。もとの配列で構築しましたが、1要素にだけ同じ操作をやればいいだけです。
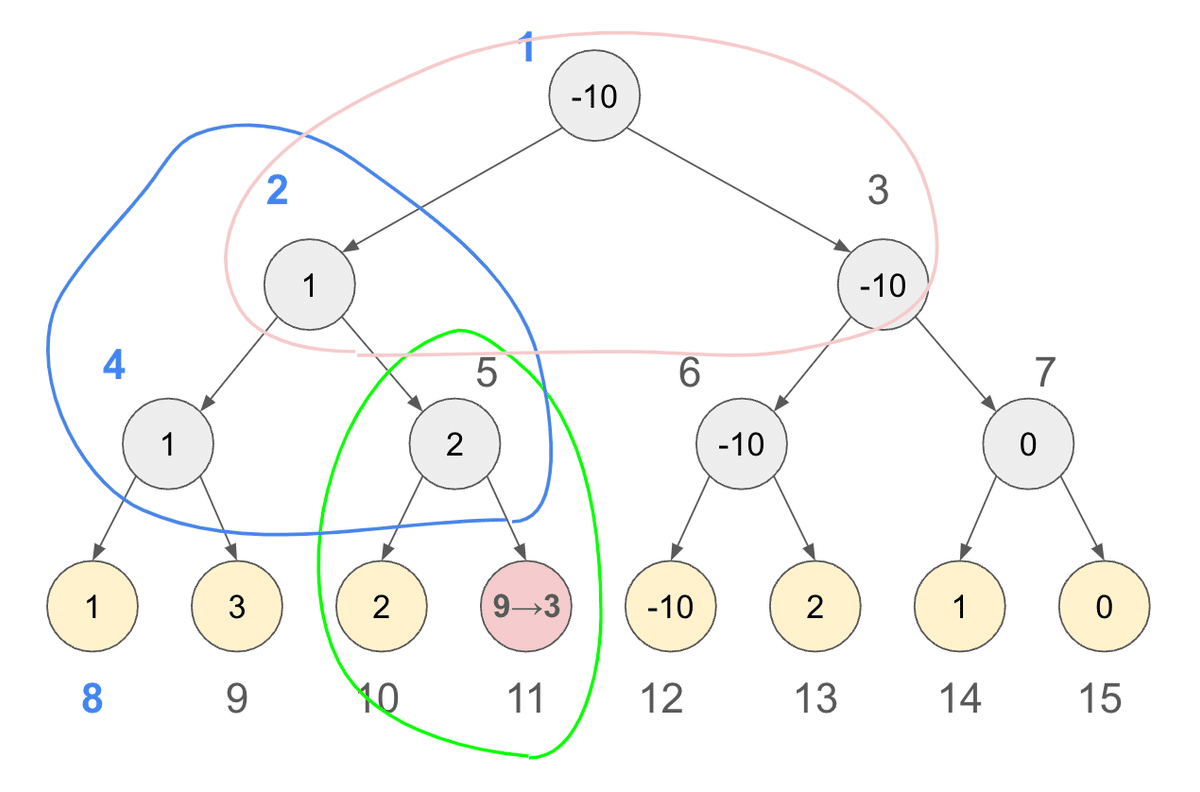
葉の値変えたので、親も変えなきゃいけません。葉にかかわりがある部分を見てみましょう。
枠でくくった3回ぶんだけ、更新が必要ですね?
これはどういうループ範囲でしょうか。
子から親に上がるには、2で割る(切り捨て)でした。
また、根まで(というか0まで)いけば、最後まで更新し切ったことになりますので
# 一点更新
idx = 3 # 元配列でのインデックス3は値9だけど
new_value = 3 # 3へ更新しよう
# まずはその葉を更新
leaf = idx + size; # 下駄はかせる
segment_tree[leaf] = new_value # 葉を更新した!
while leaf != 0:
leaf //= 2 # まずは一つ親に行って
# 親からみた子2人
child_1 = segment_tree[leaf * 2]
child_2 = segment_tree[leaf * 2 + 1]
# 小さい方を親とする
segment_tree[leaf] = min(child_1, child_2)こうなります。
「上に行って、した二つを見る」を繰り返しています。
ここまでで
構築
1点更新
ができました。いかがでしょうか?意外と単純でしょう?
セグ木の美しい構造に感動したところで、いよいよ魔法の正体を見にいきます。
2. 必要な部分だけ取得する
なんで計算量が少なく済むかというと、あらかじめ持って置いた答えを必要な部分だけ取得してるからです。
せっかく用意した木から、どうやって区間minを取得するかを説明します。
元配列のインデックス1から5までを取得することを考えます。
都合が良いので、半開区間を使わせてください。
1以上5以下でなく、1以上6未満ということです。

赤枠の最小値を知りたいです。
うーんどうやりましょう。
ここで、冒頭で使ったスプシの書き方に戻ります。

赤枠の最小値を知りたいのですが、ネタバレすると
セル選択している範囲を見れば良いです。
!?!?
なんで!?!?
いえいえ当たり前です。よくみてみましょう。
そもそも親は子2つの最小値を持っていますから
言い換えると「あらかじめ、ココからココまでの最小値を覚えておこう」を2個ずつしてるだけです。
100個値があったとして「100個の値を全部見る」のでなく、「前半の最小値は知ってて、後半の最小値も知ってる」場合、100個みますか?前半の答えと後半の答えみたらよくないですか?
ゆっくりみていきましょう
インデックス1…こいつはひとりぼっちですね。
インデックス2…親が2 ~ 3の範囲での最小値知ってます
インデックス3…親が2 ~ 3の範囲での最小値知ってます
インデックス4…親が4 ~ 5の範囲での最小値知ってます
インデックス5…親が4 ~ 5の範囲での最小値知ってます
だから、
インデックス1
2 ~ 3の範囲での最小値
4 ~ 5の範囲での最小値
の3つの最小値が、知りたい区間"1以上6未満"での最小値ということになっています。
もう少し例をみていきましょう。例えば0以上7未満で取得したい場合は

ここを見れば良いです。
なんかこう、上にビターン!! としたときの部分、です。
ちゃんと日本語で説明すると、「区間を被覆する、なるべく上にあるノード」でしょうか。まぁ伝わったと思います。伝われ。
どこを見ればいいかわかったところで、どうやって追って行けばいいか観察してみましょう。
わかりやすさのために、区間は1以上7未満でいきます。

左端のインデックスをL、右端をRとします。
Lからみていきましょう。Lはセグ木上でインデックス9ですので奇数だし、右の子です。

右の子である時、その親は範囲を超えちゃっています。

え?たまたま右の子だからじゃないかって?
安心してください。ここから先、うまいこと「右の子 = 奇数ならそれ以上親に行けない」ばかりです。
ゆっくりみていきましょう。
左端Lはこれ以上上に行けないのでインデックス9を採用するとして、次にひとつ右をみてみましょうか。

今度は「左の子」ですね。上に行けそうじゃない?行けますね?いきましょう。

ここで奇数、右の子になりました。これ以上は範囲をはみ出ちゃいますので使えません。ここでストップです。
ここまでで、採用すべき要素はここになりました。

次にまたひとつ右に行きたいのですが、ここで区間をゴールどころかはみでちゃったので、終了です。
右端からも見るので実際ははみ出ることはありません。
とりあえず行ってみたらこういうイメージになります。
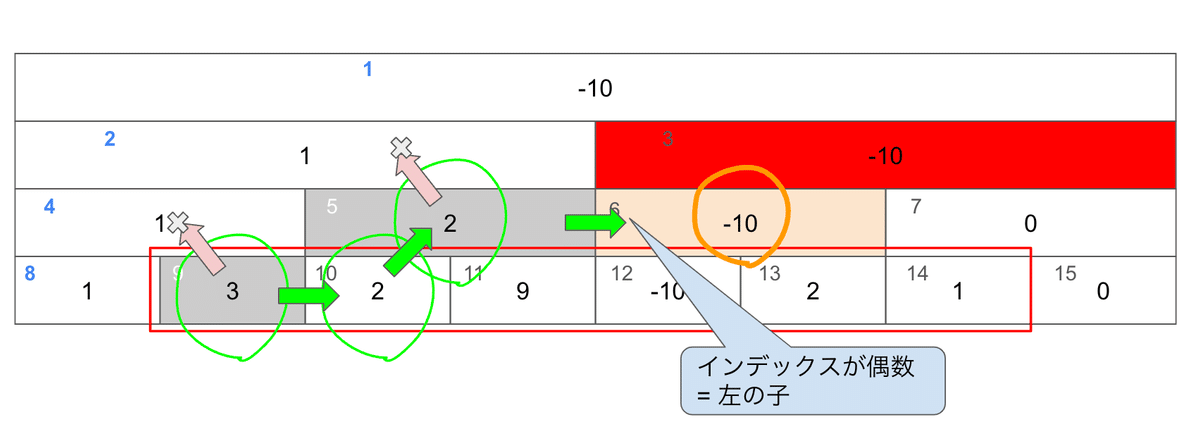
ざっくりと今までの歩き方をまとめましょう。
左端から
右の子(奇数)ならそこ採用
左の子(偶数)なら親を見る
採用したら右に進む
同じ調子で、右端からもみていきます。
まずは右端をみて...

あれ?インデックスが偶数で左の子だ、けど親は範囲飛び出てない?どうしよう...
ここで半開区間が活躍します。区間は1以上7未満ですから
赤枠の一つはみ出た右側をみます。

そしてこいつは右の子、これ以上親に上がれないので
採用するときは一つ左をみます。あくまで右端は含まないのでね。

よしよし、ではまた進んでいきます。
なるべく上に行きたいので、親を見るように進みます。
大丈夫、左端からの移動と同時にやる時、とても綺麗な処理になるので信じて進みましょう。
親に上がります。
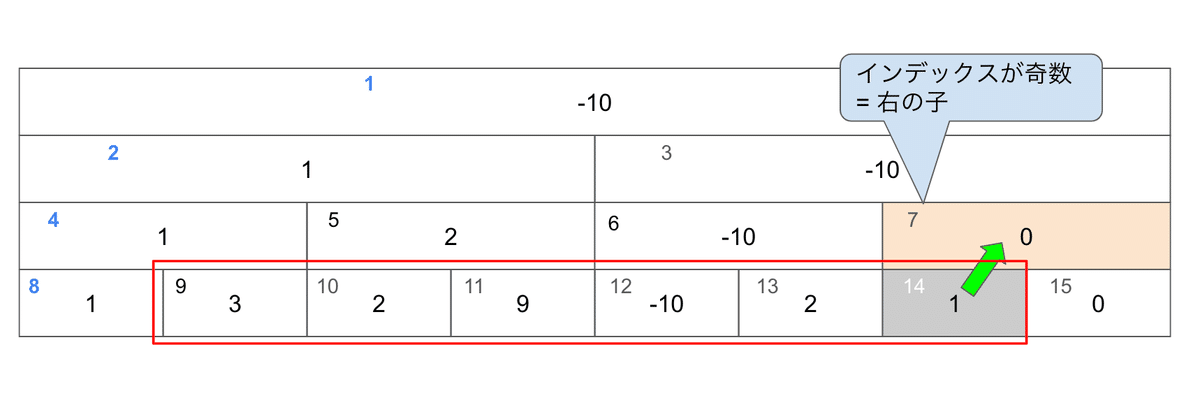
はみ出ているように見えますが、今追っている右端は「区間の一つ外側」ですので大丈夫です。
相変わらず、奇数、右の子なので採用するターンです。
一つ左を採用します。

今度は偶数なのでまた移動ターンです。いまは右端からの移動なので親に上がります。

と行きたいところですが、そろそろ本質からズレるのでいったんここまでにします。
本質は、左端・右端から同時に見ることです。
N個あったらN周なのを、logN周で済むという話をしましたね?
logN回みます。
ここからは一気に見た方が良いと思ったのでGifでみましょう。

なんと2回で終わりました。区間は6個あるので$${log_26 = 2.5849625007212...}$$ですから、だいたいlog6回でした。
話を戻すと
右の子 = インデックス奇数なら採用
左端からの場合、採用したら右(+1)に
右端からの場合、採用前に左(-1)に
1回判定したら親に(2で割る)
という動きとなっていました。これをプログラムで表現します。
# 区間取得
product = 1e9; # 何と最小値をとっても気にならない大きな数
left = 1 # idx: 1から
right = 7 # idx: 6まで、7未満を取得
# 葉のインデックスなので下駄を履かせます
left += size
right += size
# L < Rの間、繰り返します。
while left < right:
# 奇数だったら採用!
if left % 2 != 0:
product = min(product, segment_tree[left])
left += 1 # 左端の場合、採用したらひとつ右に
if right % 2 != 0:
right -= 1 # 右端の場合、ひとつ左を採用
product = min(product, segment_tree[right])
# 親にあがります。
left //= 2
right //= 2
print(product) # こたえが入っていますやったね!
これで区間の最小値の取得が少ない回数で、つまり少ない計算量で分かるようになりました。
凄まじいアイディアですね。
データ数のはなし
いままで、説明のために以下の元配列を使っていました。
dat = [1, 3, 2, 9, -10, 2, 1, 0]これは8個です。2のべき乗個です。
2べきだからセグ木が上手くいってただけなんじゃないん〜??みたいな人向けの話です。
結論から言うと何も変えずにそのまま行けます。
例えば5個の配列を見てみましょう。

いけてそうじゃない???いけるんです。
今までの考え方、コードそのままでいけます。
興味があったらひとつずつ追ってみてください。
抽象化
ここからはC++でソースを解説します。
さて、セグ木はもっと綺麗なソースになります。
ここからは2倍や2分の1を、ビット演算を使ったり
whileをforに書き換えたりします。
圧縮したものがこちら。
#include <bits/stdc++.h>
using namespace std;
constexpr int INF = 1e9;
int main() {
int N = 8;
vector<int> A = {1, 3, 2, 9, -10, 2, 1, 0};
int e = INF;
auto op = [](int x, int y) { return min(x, y); };
// 構築
vector<int> seg(N << 1, e);
for (int i = 0; i < N; ++i) seg[i + N] = A[i];
for (int i = N - 1; i >= 0; --i) seg[i] = op(seg[i << 1], seg[i << 1 | 1]);
// 1点更新
int p = 3, x = 3;
seg[p += N] = x;
while (p >>= 1) seg[p] = op(seg[p << 1], seg[p << 1 | 1]);
// 区間取得
int pd = e, l = 2, r = 6;
for (l += N, r += N; l < r; l >>= 1, r >>= 1) {
if (l & 1) pd = op(pd, seg[l++]);
if (r & 1) pd = op(pd, seg[--r]);
}
cout << pd << endl;
}綺麗になりましたね。
主に注目したいのが
1e9をeで、
minとする部分をopでまとめた
という部分です。
区間の最小値なら、1e9を入れて置いてminですが
区間の最大値が欲しかったら?
最大に関係しないほど小さな値を入れて、maxとしたいですね?
区間の和だったら?
足しても変わらない0で埋めて置いて、足し算したいですね?
そもそもセグ木は最大、最小、和、積、といろいろできますが
例えば引き算は無理です。
難しい説明になりますが、モノイドであれば載せることができます。
可換である
単位元がある
を満たせば良い。
簡単にいうと
1 + 2は、2 + 1でもいいですね?
どんな数に0足しても変わりませんね?
min(1, 2)は、min(2, 1)でもいいですね?
min(1e9, x)は、xに何入れてもxですね?(そうなるほど大きい値として1e9を採用してます。xが1e9超える可能性があるならもっと大きい値を使いましょう!)
よって
// 単位元
int e = INF;
// 二項演算
auto op = [](int x, int y) { return min(x, y); };ここだけを別枠で書くことで
おもに親子の計算などが綺麗になるし、「最小値のセグ木」「足し算のセグ木」とかでなく
「〇〇のセグ木、モノイドは別で作る」
とし、汎用的にできました。これを抽象化と言います。
構造体へ
ではstructにしましょう。
諸事情でデータ数を2のべき乗にまるめた上でサイズを確保しています。
補足ですが、インデックス1には元配列全体での計算結果が入っています。図的にあたりまえですね。
template <typename Monoid> struct SegTree {
using M = Monoid;
using T = typename M::value_type;
private:
int N, log, size;
vector<T> node;
void init() {
log = 1;
while ((1 << log) < N) ++log;
size = 1 << log;
node.assign(size << 1, M::e);
}
void update(const int &i) {
node[i] = M::op(node[i << 1 | 0], node[i << 1 | 1]);
}
public:
SegTree(int n) : N(n) {
init();
}
SegTree(const vector<T> &a) : N(a.size()) {
init();
for (int i = 0; i < N; ++i) node[i + size] = a[i];
for (int i = size - 1; i >= 1; --i) update(i);
}
T operator[](int i) {
return node[i + size];
}
vector<T> getall() {
return {node.begin() + size, node.begin() + size + N};
}
void set(int i, const T &x) {
node[i += size] = x;
while (i >>= 1) update(i);
}
void act(int i, const T &x) {
i += size;
node[i] = M::op(node[i], x);
while (i >>= 1) update(i);
}
T get(int l, int r) {
T L = M::e, R = M::e;
for (l += size, r += size; l < r; l >>= 1, r >>= 1) {
if (l & 1) L = M::op(L, node[l++]);
if (r & 1) R = M::op(node[--r], R);
}
return M::op(L, R);
}
T top() {
return node[1];
}
};
// usage sample
vector<int> dat = {1, 2, 3, 4};
SegTree<Monoid<int>> segment_tree(dat);そして、用途に応じてこんな感じでモノイド構造体を作ります。
以下は加算モノイドでの例
template <typename T> struct Madd {
using value_type = T;
static constexpr T e = 0;
static constexpr T op(const T &x, const T &y) {
return x + y;
}
};最小値ならこんな感じでしょうか。
intかlong longでinfinityの値が変わるようにしています。
template <class T> constexpr T inf = 0;
template <> constexpr int inf<int> = 1e9;
template <> constexpr long long inf<long long> = 1e18;
template <typename T> struct Mmin {
using value_type = T;
static constexpr T e = inf<T>;
static constexpr T op(const T &x, const T &y) {
return min(x, y);
}
};人それぞれ書き方が違うと思いますので、みなさん思い思いのセグメント木を生やしていきましょう。
おわりに
今回はセグメント木の仕組みを理解し
モノイドを載せて
構築$${O(N)}$$、1点更新$${O(logN)}$$、区間取得$${O(logN)}$$
が実装できるようになりました。
セグ木の植え方(構築のやり方)はほぼ紹介した意外にやり方はないと思いますが
区間取得の実装方法について差分があります。
whileループをしていることからなんとなく察している方もいるかと思いますが、再帰処理を用いることでも実現できます。
再帰での実装を紹介する記事が多いように思うのと、私は今回紹介した非再帰が好きなのでこちらを取り上げました。
興味があればいろいろセグ木をいじり、盆栽してみてはいかがでしょうか。
また、1点更新でなく、区間更新ができる進化したセグメント木双対セグメント木や遅延評価セグメント木であったり、データを2倍持たなくても良い軽量版みたいなFenwickTreeも存在します。
機会があれば紹介しようと思いますのでお楽しみに。
ALHについて知る
↓ ↓ ↓ 採用サイトはこちら ↓ ↓ ↓
↓ ↓ ↓ コーポレートサイトはこちら ↓ ↓ ↓
↓ ↓ ↓ もっとALHについて知りたい? ↓ ↓ ↓

